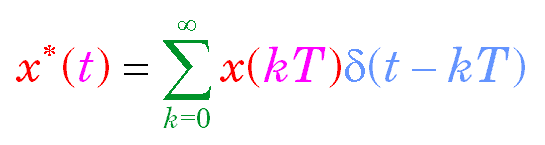
Taking the Laplace transform of the sampled signal using the integral definition and the properties of the delta function results in the following
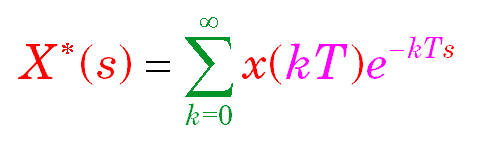
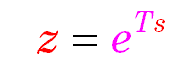
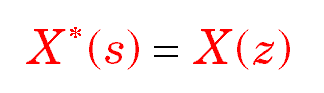

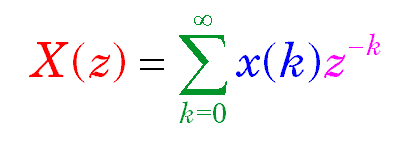
In the above equations x(kT) and x(k) represents a number arising from the sampling and digitizing process. For 8 bit quantization x(k) would have integer values from 0 to 255 (or -127 to +127) and for n bit quantization it would be from 0 to 2n - 1.
Since the Laplace variable s is complex then the variable z is also complex and X(z) is a complex function having real and imaginary parts or magnitude and phase.
Because of the increasing occurence of digital signal processing and the fact that some come into dsp without analog signal processing(considered to be mathematically difficult by some), then the above equation can be used as a definition of the Z Transform without reference to the Laplace transform.
The above definition of X(z) uses only positive values of k and is sometimes referred to as the one sided definition of the Z Transform. It is also possible to have a 2 sided definition of the transform as in the following equation. The mathematical differences between the 2 definitions mainly relate to regions of convergence. Here negative values of k will be freely included when convergence is assured.
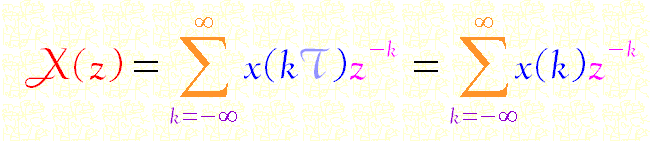
No comments:
Post a Comment